Activities
Risk-targeted intensity and behaviour factor
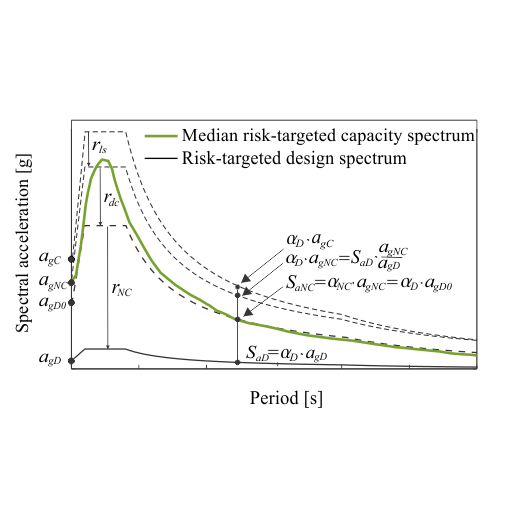
The objective is to propose risk-targeted seismic intensities which can be used for the seismic performance assessment of a structure and for the force-based design of structures against a no-collapse requirement. The proposed procedure will represent an alternative to risk-targeted hazard maps. The proposed procedure will make it possible to account for all design factors used in earthquake-resistant design of structures, and not just the seismic action. An engineer will therefore have a clearer insight into the definition of the design seismic action.
A closed form solution for risk-targeted intensity will be derived for force-based design and seismic performance assessment. The aim is to provide an insight into the risk-targeted seismic intensity, which is as a function of the target limit-state risk, the parameters of the seismic hazard, the dispersion of the seismic intensity causing a designated limit-state intensity, the ability of the structure to deform in the nonlinear range, and the over strength factor that accounts for structural redundancy and the various safety factors used in the design.
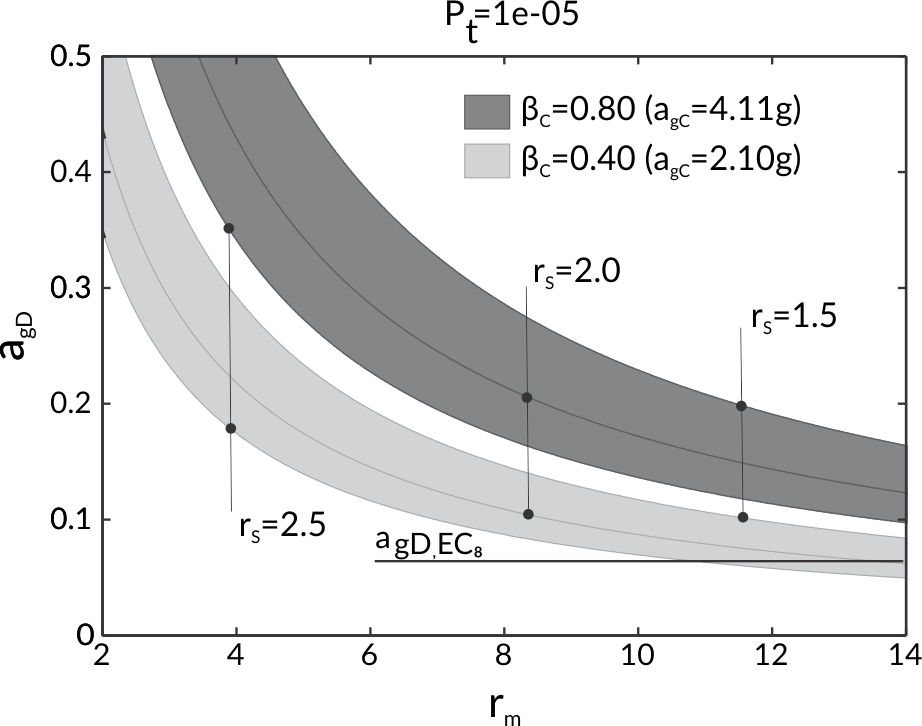
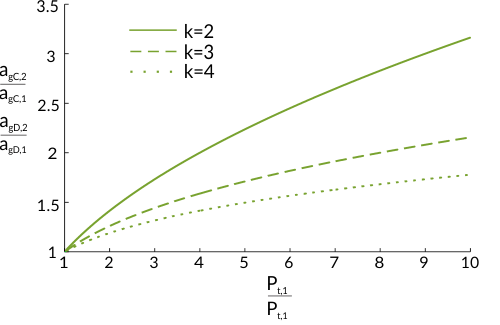
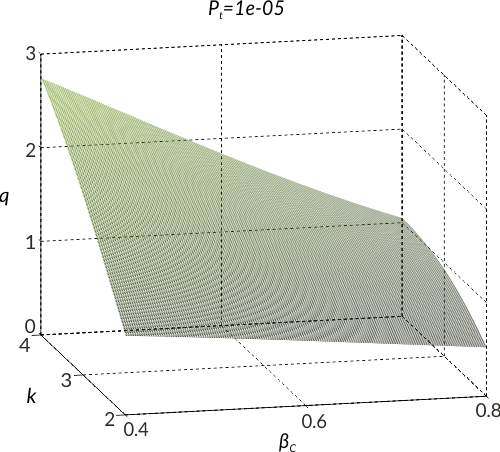
The objective is to redefine the behaviour factor using a probabilistic approach. In this case the behaviour factor is not the product of a ductility reduction factor and overstrength factor, but also depends, to a certain degree, on the target collapse risk, the dispersion of the seismic intensity causing a designated limit-state, and the return period of the seismic design action used for the design.
More details regarding this study are available in the paper.
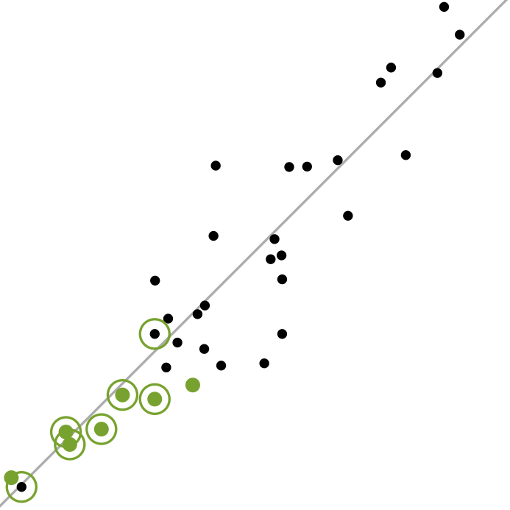
3R method
- Response analysis, Record selection, Risk-based decision makings
- Realization of concept of Intensity-based assessment for risk-targeted decision making
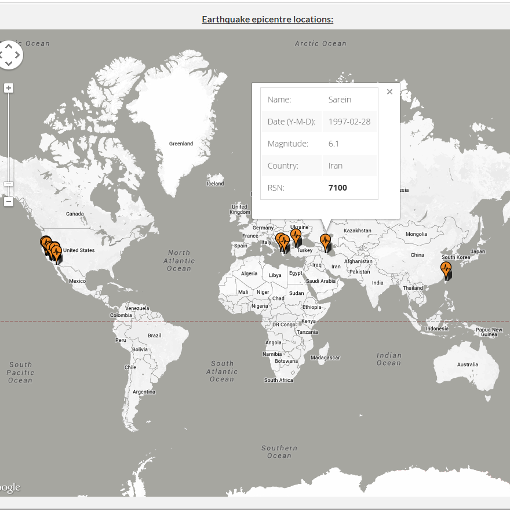
CGM webapp
- Online application for selection of Characteristic Ground Motions
- Database contains > 18.000 ground motions