SeisMic Analysis & Risk-Targeted engineering

Intensity bounds and seismic risk

Risk-based performance objectives have become a part of the seismic design of structures. Thus it is important to develop procedures for the accurate assessment of the seismic risk. When integrating the seismic risk equation in order to estimate, for example, the collapse risk, the question arises as to which are the adequate integration limits? For example, a well-known closed-form solution of the risk equation has been derived by integrating the risk integral over the entire range of intensities, namely from zero to infinity.

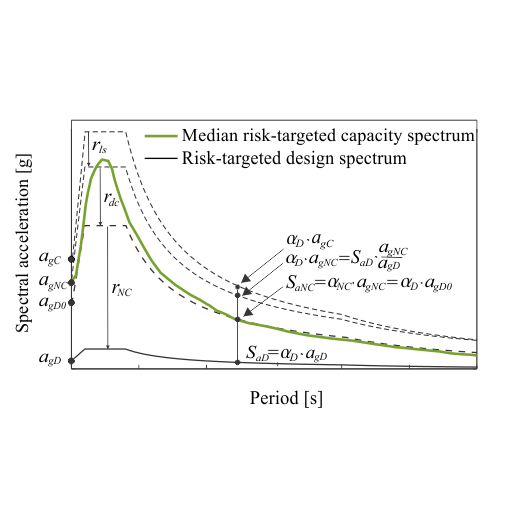
Such approach is not physically consistent since a lower and upper bound of seismic intensity exist. The lower bound $im_1$ is defined as the minimum ground-motion intensity which causes a designated limit state in a structure, and can be estimated on the basis of dynamic analyses. The upper bound $im_2$ is, in general, related to the physics of earthquakes, the tectonic regime, and the geology of the terrain, and can be interpreted as being the maximum possible intensity at an observed location or as a design value, defined, for example, for a chosen return period. However, the upper bound of ground-motion intensity is not necessarily the physical limit of the intensity, since risk communication in the case of the design of ordinary structures may also be based on the risk conditioned to the upper bound intensity associated with a low rate of occurrence.

The impact of the lower and upper bounds depends on the slope of the seismic hazard curve ($k$) and the log-normal distribution of intensities causing a selected limit state, and also on the chosen measure of seismic intensity, e.g. the peak ground acceleration ($a_g$) or the spectral acceleration ($S_a$). The impact of the lower ($a_{g1}$, $S_{a1}$) and upper intensity bound ($a_{g2}$, $S_{a2}$) is not always negligible, and by not taking into account their effect, the seismic risk can be highly overestimated (i.e. cases when $\Delta\lambda \ll 1$). More details regarding this study are available in the paper.

The impact of the lower intensity bound ($\Delta\lambda_{C,ag1}, \Delta\lambda_{C,Sa1}$) and the upper intensity bound ($\Delta\lambda_{C,ag2}, \Delta\lambda_{C,Sa2}$) on the probability of collapse for six observed structures and two intensity measures, peak ground acceleration ($a_g$) and spectral acceleration ($S_a$).

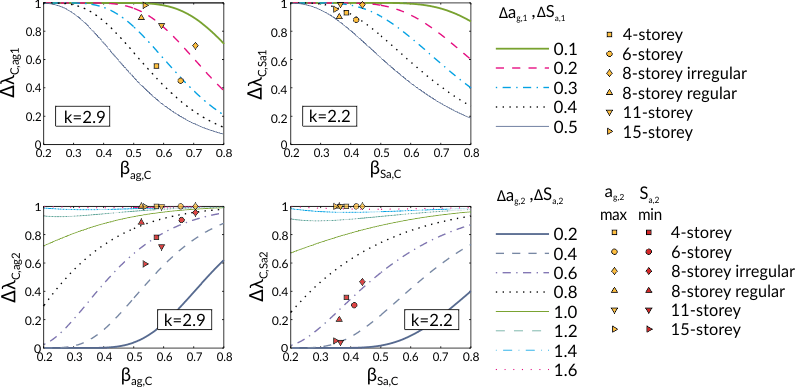
A new closed-form equation for seismic risk estimation, which takes into account intensity bounds, was derived in order to predict seismic risk more accurately. A linear hazard curve in log-log coordinates and a lower bound truncated log-normal distribution of intensities causing a selected limit state were taken into account. Additionally, the equation was derived by integrating from the lower bound $im_1$ to the upper bound of intensity $im_2$. Details are available in the paper.